Buch lesen: "Логика для всех. От пиратов до мудрецов", Seite 2
Занятие 2
Урок русского языка, или «Все», «некоторые» и отрицание
…о великий, могучий, правдивый и свободный русский язык!
И. С. Тургенев. «Русский язык»
Предмет этого занятия – общие и частные высказывания. В формальной логике для их записи используют всего два квантора (квантор общности V и квантор существования 3). А в бытовом языке вместо кванторов используют самые разные слова, что порой приводит к недоразумениям. Задачи 2.1, 2.2 и 2.13 помогают разобраться в способах передачи кванторов общности и существования средствами русского языка.

Смысл общих и частных высказываний удобно иллюстрировать с помощью кругов Эйлера. Рекомендуем их использовать при обсуждении задач 2.3, 2.11, 2.12, 2.16, несмотря на то что для решения предложенных задач часть учеников в иллюстрациях не нуждается. Во-первых, другой части учеников картинка может существенно помочь. Во-вторых, навык работы с кругами Эйлера еще никому не повредил. Надеемся, что в задаче 2.16 удобство трех кругов оценят и те, кому два круга в предыдущих задачах казались излишним «наворотом». В-третьих, использование кругов Эйлера позволяет почувствовать родство логики и теории множеств.
Задачи 2.4–2.10, 2.14, 2.15 связаны с построением отрицания к общим и частным высказываниям. Меньше всего нам бы хотелось, чтобы итогом занятия стала формулировка соответствующей пары правил, которое дети будут потом применять в задачах. А больше всего – чтобы они грамотно строили отрицания, не задумываясь о правилах. Если на этом занятии дети много ошибаются, продолжайте предлагать на последующих занятиях аналогичные упражнения (в том числе из раздела дополнительных задач) до победного конца.
Можно ли одну и ту же мысль выразить по-разному? Насколько сильно зависит смысл русского предложения от порядка слов? Всегда ли одинаково следует понимать одни и те же слова? Не будем пытаться на одном занятии изучить весь русский язык. Ограничимся несколькими словами и выражениями: «все», «каждый (любой)», «некоторые», «существует», «хотя бы один».
Задача 2.1. 1) Серый Волк заинтересовался цветом шапочек. Однажды он встретил Красную Шапочку. Помогите Волку сделать правильный вывод. Придумайте несколько вариантов.
2) Выразите другими словами мысль «Все шапочки красные».
Решение. 1) Можно сказать: «Некоторые шапочки красные». Но можно и по-другому. Например, так:
Шапочки бывают красные.
Иногда встречаются красные шапочки и т. п.
Математики любят говорить точно: «Существует хотя бы одна красная шапочка».
2) «Шапочки всегда красные», «Любая шапочка красная» или «Каждая шапочка красная».
Задача 2.2. Вася говорит, что слова «для всех» и «для каждого» означают одно и то же. Прав ли Вася?
Решение. Вопрос скорее лингвистический, чем математический. Часто смысл предложения действительно не меняется при замене «для всех» на «для каждого» и соответствующих изменениях формы слов. Например, «Для всех принцесс горошины под периной невыносимы» означает то же, что и «Для каждой принцессы горошина под периной невыносима». Но вот если вместо «Выдать зимовщикам для всех одну пару валенок» попросить «Выдать зимовщикам для каждого одну пару валенок», зимовщики наверняка заметят разницу.
Задача 2.3. 1) Означают ли одно и то же высказывания: «Некоторые сантехники любят рэп» и «Некоторые любители рэпа – сантехники»?
2) Означают ли одно и то же высказывания: «Все сантехники любят рэп» и «Все любители рэпа – сантехники»?
Ответ. 1) Да. 2) Нет.

Рис. 1
Решение. 1) Чтобы лучше разобраться в смысле высказываний, изобразим их с помощью кругов Эйлера (см. рис. 1). Пусть в одном круге находятся сантехники, в другом – любители рэпа. Если первое высказывание истинно, то круги непременно пересекаются, и в пересечении кругов располагается хотя бы один сантехник, любящий рэп. Но ровно это же требуется и для истинности второго утверждения. Поэтому они означают одно и то же.
2) Снова разместим сантехников и рэперов в пересекающихся кругах. В пересечении кругов, как и прежде, расположены сантехники, любящие рэп. Сантехники, НЕ любящие рэп, окажутся в серой части рисунка 2. Если таковых нет (т. е. все сантехники любят рэп), то серая часть пуста.

Рис. 2
Чтобы показать это на рисунке, принято изображать круг сантехников внутри круга рэперов (см. рис. 3).
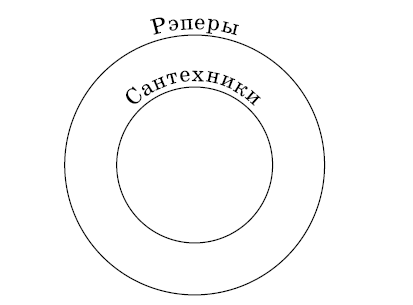
Рис. 3
Сравнение рисунков 3 и 4 помогает понять, почему смысл высказываний «Все сантехники любят рэп» и «Все любители рэпа – сантехники» разный.

Рис. 4. Все любители рэпа – сантехники
Задача 2.4. Лжец сказал: «В этой корзине все грибы съедобны». Значит ли это, что все грибы в этой корзине ядовиты? (Для простоты забудем об условно съедобных грибах и будем каждый гриб считать либо съедобным, либо ядовитым.)
Ответ. Нет, не значит. В корзине могут лежать одновременно и съедобные, и ядовитые грибы.
Обсуждение. Неверно, что все грибы съедобны. Значит, съедобны НЕ ВСЕ грибы. То есть ХОТЯ БЫ ОДИН из грибов ядовит.
Задача 2.5. Рассмотрим два утверждения. Сколько из них могут быть верными?
1) В этой корзине все грибы съедобные.
2) В этой корзине есть хотя бы один ядовитый гриб.
Ответ. Верно ровно одно утверждение.
Решение. Начнем внимательно перебирать грибы по одному. Первый же найденный нами ядовитый гриб окажется одновременно и контрпримером, опровергающим первое высказывание, и примером, подтверждающим второе. А если, перебрав всю корзину, ядовитого гриба мы так и не найдем, то верным окажется только первое утверждение. В любом случае одно из двух утверждений истинно, а другое ложно.
Комментарий. Почему так получилось? Потому что утверждения «В этой корзине все грибы съедобные» и «В этой корзине есть хотя бы один ядовитый гриб» противоположны, то есть одно из них является отрицанием другого. А по закону исключенного третьего в этом случае как раз и верно ровно одно из двух.
Итак, чтобы построить отрицание к высказыванию про всех, надо заменить:
• «всех» на «некоторых»;
• свойство на противоположное (например, «ядовитое» на «съедобное»).
Задача 2.6. Лжец сказал: «В этой корзине некоторые грибы ядовитые». Что можно узнать из этого высказывания?
Решение. Если бы в корзине был хотя бы один ядовитый гриб, лжец был бы прав. Поэтому ядовитых грибов в корзине нет. Другими словами, все грибы в этой корзине съедобны.
Итак, чтобы построить отрицание к высказыванию про некоторых, надо заменить:
• «некоторых» на «всех»;
• свойство на противоположное (например, «ядовитое» на «съедобное»).
Задача 2.7. Дано утверждение: «Все малышки хорошо поют». Незнайка сформулировал к нему отрицание: «Все малышки поют отвратительно».
1) Как с помощью закона исключенного третьего убедить Незнайку, что он ошибся?
2) Сформулируйте отрицание правильно.
Решение. 1) По закону исключенного третьего верно ровно одно из двух: либо утверждение, либо его отрицание. Найдя двух малышек, одна из которых поет хорошо, а вторая плохо, мы убедимся, что неверно ни само утверждение, ни его «отрицание», придуманное Незнайкой.
2) «Существует хотя бы одна малышка, которая поет плохо». Или «Некоторые малышки поют плохо».
Задача 2.8. Постройте отрицания к каждому утверждению, не используя частицу «не». Где сможете, укажите, что верно: утверждение или его отрицание. Где сможете, обоснуйте свое мнение примером или контрпримером.
1) На Земле существует хотя бы одна гора выше 10000 м над уровнем моря.
2) Существует хотя бы один вулкан с высотой более 10000 м относительно своего основания.
3) Любой жук помещается в спичечном коробке.
4) Некоторые горные реки быстрые.
5) Бутерброд всегда падает маслом вниз.
Ответ. 1) Верно отрицание: любая гора на Земле не выше 10000 м над уровнем моря. Обосновать утверждение такого типа примером нельзя, знание высоты Эвереста (8848 м) не доказывает, что более высоких гор нет.
2) Верно утверждение. Пример – вулкан Мауна-Кеа на Гавайских островах с высотой 10203 м от основания (и «всего» 4205 м над уровнем моря). Последний раз этот вулкан извергался несколько тысяч лет назад. А самый высокий вулкан Солнечной системы – гора Олимп на Марсе имеет высоту 21,2 км от основания.
3) Верно отрицание: существует хотя бы один жук, не помещающийся в спичечном коробке. Пример – жук-голиаф из подсемейства бронзовки, обитающий в Африке. Длина его тела достигает 11 см.
4) Верно утверждение. Примером служит любая горная река.
5) Не стоит относиться к этой задаче всерьез. Для точного построения отрицания потребуется сначала строго определить, что такое бутерброд. Например, может ли он вообще не содержать масла? Мы предполагаем, что при любом определении верным окажется отрицание, но для приведения примера может потребоваться тренировка.
Задачи для самостоятельного решения
Задача 2.9. Рассмотрим два утверждения:
А: В этой корзине все грибы съедобные.
Б: В этой корзине есть хотя бы один съедобный гриб.
Могут ли быть верными: 1) оба утверждения; 2) ровно одно из них; 3) ни одного?
Задача 2.10. Является ли высказывание «В этой корзине некоторые грибы съедобные» отрицанием высказывания «В этой корзине некоторые грибы ядовитые»?
Задача 2.11. Нарисуйте с помощью кругов Эйлера иллюстрацию к каждому высказыванию. Есть ли среди иллюстраций одинаковые? Одинаков ли смысл соответствующих высказываний?
1. Все хоббиты живут в норах.
2. Все жители нор – хоббиты.
3. Некоторые кошки серые.
4. Некоторые серые существа – кошки.
Задача 2.12. Когда учительница ругала Дениса за плохой почерк, он сказал: «У всех великих людей был плохой почерк, значит, я великий человек». Прав ли он?
Задача 2.13. Шерлок Холмс допросил Зайца, Волка и Лису по делу о съедении Колобка. Подозреваемые заявили:
Заяц: «Хотя бы один из нас съел Колобка».
Волк: «Хотя бы один из нас не ел Колобка».
Лиса: «Хотя бы один из нас сказал правду».
Как известно, Колобка съела Лиса. Кто сказал правду, а кто солгал?
Задача 2.14. Комиссия посетила больницу и составила отчет, в котором не было ни одного правдивого утверждения.
«Все врачи имеют достаточный опыт. Некоторые врачи никогда еще не ставили неправильного диагноза. Никто из врачей не опаздывает на работу. Все пациенты довольны лечением. Ни один из них не жалуется на бытовые условия. Некоторые пациенты выздоравливают за один день».
Напишите, как выглядел бы честный отчет.
Задача 2.15. В комнате собрались несколько жителей острова рыцарей и лжецов. Трое из них сказали следующее:
– Нас тут не больше трех человек. Все мы лжецы.
– Нас тут не больше четырех человек. Не все мы лжецы.
– Нас тут пятеро. Лжецов среди нас не меньше трех.
Сколько в комнате человек и сколько из них лжецов?
Задача 2.16. Предположим, что справедливы следующие утверждения:
• Среди людей, имеющих телевизоры, не все являются малярами.
• Люди, каждый день купающиеся в бассейне, но не являющиеся малярами, не имеют телевизоров.
Следует ли отсюда, что не все владельцы телевизоров каждый день купаются в бассейне?
Занятие 3
Вдоль по Африке, или Примеры для некоторых и контрпримеры для всех
Но папочка и мамочка уснули вечерком,
А Танечка и Ванечка – в Африку бегом, —
В Африку!
В Африку!
К. И. Чуковский
Школьники часто начинают решение задачи с поиска подходящего примера. Но тут встают три вопроса. Как такой пример подобрать? В каких случаях достаточно привести один пример для полного решения задачи? Что делать в остальных случаях? На этом занятии мы постараемся научиться отвечать на самый простой вопрос, но от этого не менее важный: на второй. Умение отличать решенную задачу от нерешенной – основа математической культуры. Отвечать на первый вопрос помогут другие выпуски нашей серии, а на третий – только годы занятий.

При составлении этого занятия мы вновь постарались учесть интересы разнородного по составу кружка. Вопрос применимости примеров и контрпримеров актуален прежде всего для начинающих, сложность задач для самостоятельного решения на приведение примера разнообразна, а рассуждения про пустое множество и парадоксы про Деда Мороза достаточно сложны. Чисто логические вопросы можно разбавить конструктивами по вкусу.
Во введении обсуждается применимость примеров (в том числе контрпримеров) к доказательству и опровержению частных и общих высказываний. Истинность таких высказываний предлагается определить и в большинстве задач. Но мы сознательно нарушили чистоту жанра, включив в занятие задачи 3.6 и 3.7 с вопросом «можно или нельзя?», в которых фактически требуется определить, что верно: частное высказывание или его отрицание.
Надеемся, что пяти- и шестиклассникам будет интересно разыграть сценку с Танечкой и Ванечкой в начале занятия. Текст четырем «артистам» стоит выдать заранее, но учить его наизусть незачем, пусть подглядывают в шпаргалки. Таблицу рекомендуем изобразить на доске, можно с сокращениями.
Более опытных кружковцев могут заинтересовать два сюжета. Первый связан с гипотезами Гольдбаха (задача 3.2). Это уникальный случай, когда формулировка совсем недавнего выдающегося математического достижения понятна школьнику. Участники кружка могут совместными усилиями проверить гипотезу Гольдбаха для чисел из первой сотни (если каждому поручить свой отрезок числового ряда), осознать необходимость доказательства, а затем узнать историю проблемы и вместе порадоваться успеху Хельфготта.
Второй тонкий вопрос – это истинность любого общего высказывания об элементах пустого множества (задачи 3.3–3.5 и 3.12). В школьной программе он игнорируется из-за несоответствия формального и житейского подхода к нему. Это приводит к неоднозначному толкованию условия некоторых задач (в частности, с параметром). Несложная задача 3.11 служит для повторения материала предыдущего занятия, а ее сюжет связан с гораздо более сложной следующей задачей-парадоксом 3.12.
Задача 3.13 позволяет эффектно завершить занятие. Она не имеет отношения к его теме, содержательно в ней развивается наиболее сложная идея первого занятия, а сюжетно – линия Деда Мороза. Можно в начале занятия не выдавать ее вместе с другими задачами, а дать «на сладкое» двум кружковцам, решившим другие задачи быстрее остальных. В задаче 3.12 обсуждается существование Деда Мороза. После этого самое время выпустить «на сцену» двух «артистов», которые неопровержимо докажут существование Деда Мороза!
Однажды Танечка и Ванечка услышали про Африку. И подумали, что в Африке водятся большие звери. Они дождались, когда мама с папой уснули, и убежали в Африку. Там Танечка успела увидеть только мартышку, а Ванечка бегемота. Тут как раз проснулись родители. Они обо всем догадались и забрали детей из Африки домой. На обратном пути дети заспорили.
– Правда, африканские звери большие? Я же сам видел! – спросил у папы Ваня.
– Нет, африканские звери маленькие, – не соглашалась Таня. – Я тоже сама видела. Вот скажи, папа, кто из нас прав?
– А это смотря как понимать вопрос, – начал папа. – Можно так: «Верно ли, что НЕКОТОРЫЕ африканские звери большие?»
– Да, верно! – торжествующе посмотрел на сестру Ваня. – Например, бегемот, которого я видел.
– Молодец, – похвалил папа. – Для ответа «Да» на вопрос про некоторых достаточно привести один пример.
– А если бы я не увидел бегемота? – забеспокоился Ваня. – Тогда из-за Танькиной мартышки ответ был бы «Нет, неправда»?
– Ну что ты! – успокоил его папа. – Размеры животных не зависят от того, видишь ли ты их. Даже если встретишь тысячу маленьких мартышек, отвечать «Нет» еще рано. Понимаешь почему?
– Понимаю, – сказал Ваня. – Бегемот или другой пример мог просто хорошо спрятаться!
– Поэтому ответ «Нет» на вопрос про некоторых объяснить бывает непросто, – вздохнула мама. – Для этого требуется настоящее доказательство.
А папа продолжил:
– Но ваш вопрос можно понять и совсем по-другому: «Верно ли, что ВСЕ африканские звери большие?».
– Откуда мы знаем? Мы же не успели увидеть всех зверей, – начал было Ваня, но Танечка его перебила:
– А вот и знаем! Не все. Ведь я же видела маленькую мартышку!
– Хорошо, что ты ее увидела, – похвалил папа. – Твоя мартышка – прекрасный…
– Пример! – перебила Танечка.
– Почти, – согласился папа. – Только пример, который помогает опровергнуть предположение, называется КОНТРПРИМЕР. И для ответа «Нет» на вопрос про всех достаточно привести один контрпример.
– А если ответ был бы «Да»? – хором спросили дети. – Как называется нужный пример?
– Никак не называется, – ответил папа. – Потому что его нет. Никакими примерами не убедишь, что где-нибудь ВСЕ звери большие.
– Поэтому ответ «Да» на вопрос про всех объяснить бывает непросто, – вздохнула мама. – Для этого требуется настоящее доказательство.
– А если ты уже тысячу зверей встретил и все они большие? – с надеждой спросил Ванечка.
– Ну и что! – победно вскричала Танечка. – Хоть миллион! Моя маленькая мартышка тем более могла спрятаться! Еще получше твоего бегемота!
Пока Танечка и Ванечка выясняют, кто лучше прячется, опишем с помощью таблицы два типа утверждений:

Там, где стоят знаки вопроса, общего рецепта нет, для каждой задачи приходится искать свое доказательство.
Задача 3.1. Определите, какие из утверждений верны. Где можно, подтвердите свой ответ примером (контрпримером). В остальных случаях обоснуйте его по-другому.
1. Все нечетные числа простые.
2. Все простые числа нечетные.
3. Некоторые нечетные числа простые.
4. Некоторые простые числа нечетные.
5. Все четные числа составные.
6. Все числа вида р + 7, где р – простое, являются составными.
Ответ. Верны утверждения 3, 4, 6.
Решение. Привести контрпримеры к утверждениям 1, 2, 5 и примеры к утверждениям 3, 4 предоставляем читателю. Для доказательства утверждения 6 рассмотрим два случая. Если р = 2, то число р + 7 = 9 – составное. Если простое число p ≠ 2, то оно нечетное, поэтому р + 7 – четное и больше 2, следовательно, составное.
Задача 3.2. Верно ли высказывание: «Любое нечетное число, большее 5, можно представить в виде суммы трех простых чисел»?
Обсуждение. На первый взгляд это утверждение мало отличается от сформулированных в предыдущем задании. Попробуем рассуждать так же. Для начала поищем контрпример (как в пунктах 1, 2 и 5 предыдущей задачи): 7 = 2 + 2 +3, 9 = 3 + 3 +3, 11 = 3 + 3 + 5 и т. д. Не получается? Что ж, попытаемся доказать, что утверждение верно (как в пункте 6). Тоже не получается? Не огорчайтесь, вы не одиноки! Еще в 1742 году Кристиан Гольдбах предложил эту задачу Леонарду Эйлеру. Позже она получила название тернарной проблемы Гольдбаха. Ей занимались многие математики, но лишь в 2013 году американский математик Харальд Хельфготт окончательно доказал, что гипотеза Гольдбаха верна. А бинарная проблема Гольбаха, упоминавшаяся на первом занятии, не решена до сих пор.
Задача 3.3*. Верно ли утверждение: «Все дожившие до наших дней тираннозавры умеют вышивать крестиком»?
Обсуждение. Утверждение звучит странно и на первый взгляд кажется неверным. Что ж, попробуем его опровергнуть. Для этого нужно привести контрпример – то есть дожившего до наших дней тираннозавра, не умеющего вышивать крестиком. Поскольку его не существует, то утверждение верно.
Ответ. Да, верно.
Комментарий 1. Сравним две последние задачи. Поиск контрпримера в обеих оказался затруднительным. Но эти затруднения разного характера. Контрпример к проблеме Гольдбаха мы найти не могли, но не были уверены, что его не сможет найти кто-то более умный или терпеливый. Поэтому вывода сделать не могли (а Харальд Хельфготт смог!). А вот живого тираннозавра не только мы с вами не можем найти, но и уверены, что никто другой не найдет.
Комментарий 2. Аналогично можно верно высказываться не только о живых тираннозаврах, но вообще обо всем, чего на самом деле нет. Например, все кролики, проглотившие удава, остались голодными. (Не верите? Тогда найдите кролика, проглотившего удава, и поинтересуйтесь, сыт ли он.) А все четные числа, оканчивающиеся на 5, оканчиваются на 7. С точки зрения формальной логики любое высказывание обо всех элементах пустого множества верно, потому что к нему не может быть приведен контрпример.
Есть и другая причина считать верными высказывания о современных тираннозаврах и прочих несуществующих объектах. Начнем с несомненно истинного высказывания «Все числа, кратные 12, четны». Дополнив условие, мы получим следствие из него, которое тоже должно быть истинным. Например, «Все трехзначные числа, кратные 12, четны». Или «Всякое число с суммой цифр 30, кратное 12, четно». Или «Всякое число с суммой цифр 100, кратное 12, четно». А теперь заметим, что числа с суммой цифр 100, кратные 12, – такие же несуществующие объекты, как и современные тираннозавры.
Задача 3.4*. Рассмотрим два высказывания:
А: Некоторым Мишиным одноклассникам 12 лет.
Б: Всем Мишиным одноклассникам 12 лет.
Можно ли, ничего не зная про Мишу, утверждать, что:
1) если верно А, то верно и Б;
2) если верно Б, то верно и А?
Обсуждение. Если бы речь шла об одном конкретном Мише, вопрос был бы неинтересен. Например, Миша учится в шестом классе, у него двадцать одноклассников и всем им по 12 лет; тогда оба высказывания, А и Б, истинны. Однако в задаче требуется понять, может ли для какого-нибудь Миши первое высказывание оказаться верным, а второе нет (т. е. возможен ли контрпример).
Решение. 1) Нельзя. Контрпример очевиден: пусть у Миши 5 (или любое другое натуральное число) одноклассников, которым двенадцать лет, и 20 (или любое другое натуральное число) тринадцатилетних одноклассников. Тогда А истинно, а Б ложно.
2) Как ни странно, тоже нельзя! Для построения контрпримера предположим, что Мише три года, и никаких одноклассников у него вообще нет. Верно ли утверждение Б? Верно! Кто не согласен, пусть предъявит контрпример – Мишиного одноклассника другого возраста. А утверждение А, означающее, что существует хотя бы один Мишин двенадцатилетний одноклассник, неверно.
Задачи для самостоятельного решения
Задача 3.5. Землянин Вася сказал: «Все марсиане лжецы». Прав ли Вася?
Задача 3.6. Есть 30 гирек, которые весят 1 г, 2 г, 3 г, …, 30 г. Можно ли разложить их: 1) на две кучки одинакового веса; 2) на три кучки одинакового веса?
Задача 3.7. 1) Можно ли заполнить таблицу 3x3 натуральными числами так, чтобы сумма чисел в каждой строке была четным числом, а в каждом столбце – нечетным? 2) А таблицу 4x4?
Задача 3.8. Верно ли, что периметр любого четырехугольника, целиком находящегося внутри данного квадрата, меньше периметра этого квадрата?
Задача 3.9. Верно ли, что все числа вида 2n + 15, где n – натуральное число, простые?
Задача 3.10. Рассмотрим натуральные числа, в записи которых нет нулей.
1) Найдется ли среди них десятизначное число, делящееся на сумму своих цифр?
2) А стозначное?

