Buch lesen: «Математические модели в естественнонаучном образовании. Том II»

Schriftart:

Глава 5. Построение филогенетических деревьев

Смоделировав эволюцию ДНК в предыдущей главе, теперь готовы использовать эти модели для важных выводов из реальных данных ДНК. Увидим, как модель молекулярной эволюции вместе с некоторыми новыми математическими методами может быть использована для восстановления хронологии событий эволюционной истории. Давайте рассмотрим хорошо изученный, но все же удивительный вопрос: кем приходятся люди современным обезьянам? Более точно, какие из горилл, шимпанзе, орангутанов и гиббонов являются нашими ближайшими эволюционными родственниками, или все эти обезьяны более тесно связаны друг с другом, чем с нами?

Рисунок 5.1. Две возможные филогении гоминоидов.

Ранние эволюционисты рассматривали шимпанзе и горилл как наших ближайших родственников. Считалось, что люди и эти африканские обезьяны образуют одну эволюционную группу, которая отделилась от других линий обезьян в более отдаленном прошлом. Чуть позже господствующим стало мнение, что все современные человекообразные обезьяны более тесно связаны друг с другом, чем с людьми. Две возможные схемы, представляющие более подробные версии этих конкурирующих взглядов на эволюцию гоминоидов, показаны на рисунке 5.1.

Вопросы для самопроверки:

– Поскольку шимпанзе и горилла являются африканцами, в то время как орангутанг и гиббон являются азиатами, что, если вообще что-либо, каждое из этих деревьев укажет о вероятном месте появления первых людей?

Как выбрать, какое из этих или многих других возможных эволюционных деревьев является лучшим описанием происхождения гоминоидов? Один из подходов заключается в том, что сначала выбирают конкретный ген, общий для всех человекообразных обезьян и людей, но последовательность ДНК которого показывает вариации от вида к виду. Если предположить, что этот ген является общим и сходным для всех гоминоидов, поскольку он произошел от общего предка (то есть последовательности ортологичны, другими словами, к их разделению привел процесс видообразования), то вариации последовательностей среди видов должны содержать информацию об их эволюционной истории.

Например, 898-элементные пары последовательностей митохондриальной ДНК HindIII из этих гоминоидов и семи других приматов были зарегистрированы в работе Хаясака с соавторами 1988 года, он в свою очередь опирался на работу коллективов под руководством Андерсона 1981 года и Брауна 1982 года. Эти последовательности согласуются на 67-97% участков, в зависимости от того, какие из них сравниваются. Чтобы увидеть эти последовательности, загрузите базу данных primatedata в MATLAB, а затем посмотрите имена переменных, в которых они хранятся.

Хотелось бы вывести филогенетическое дерево, подобное одному из представленных на рисунке 5.1, показывающее, как все обезьяны эволюционировали от общего предка. Но какие данные указывают на «лучшее» дерево или даже «хорошее» дерево, чтобы объективно описать эволюционное происхождение?

Конечно, ученые уже рисовали деревья, показывающие подозрительные эволюционные отношения между видами задолго до появления методов секвенирования ДНК. Морфологическое сходство между видами является одним из источников подсказок относительно того, какие деревья адекватно описывают происхождение видов. Идентификация общих предков по окаменелостям – это другой подход. Теперь данные последовательности предоставляют новый источник информации об эволюционной истории, но использование их для вывода филогенетических деревьев требует разработки новых математических инструментов.

5.1. Филогенетические деревья

Прежде чем начнем разрабатывать методы построения филогенетических деревьев, понадобится некоторая терминология. Поскольку последовательности, которые, возможно, захотим связать, могут происходить от разных видов, как в примере с гоминоидами, или вместо этого от разных подвидов, популяций или даже отдельных особей, будем называть каждый источник последовательности ДНК таксоном (множественное число таксоны). Эквивалентный общеупотребительный термин – операционная таксономическая единица, обычно обозначаемая аббревиатурой ОТЕ (в иностранной литературе можно встретить обозначение OTU).

Будет стараться нарисовать диаграмму, состоящую из отрезков линий, которая представляет собой эволюционную историю таксонов. Каждый из сегментов линии на диаграмме по устоявшейся в теории графов терминологии называется ребром. Диаграмма, подобная приведенной выше, в которой нет циклов и петель, образованных ребрами, называется деревом.

Вопросы для самопроверки:

– Почему разумно предположить, что эволюционные отношения могут быть смоделированы путем рисования именно деревьев? Что бы это значило, если бы существовали цикл или петля?

Поскольку существует боковой перенос генов, например, когда вирусная ДНК постоянно включается в ДНК хозяина, деревья не могут описать все эволюционные отношения. Они обеспечивают простейшую модель, которая, тем не менее, полностью адекватна для большинства применений.

Точка, в которой сходятся нескольких ребер называется внутренней вершиной, в то время как висячий конец ребра у таксона называется конечной вершиной или листом дерева. Вершина, в которой будет находиться общий предок всех таксонов, называется корнем.

Говорят, что дерево раздваивается, находится в состоянии бифуркации, если на каждой его внутренней вершине встречаются по три ребра, а у корня сходится два ребра, как на деревьях на рисунке 5.1. Такие деревья называют двоичными или бинарными. Хотя с биологической точки зрения возможно, что дерево, отличное от двоичного, могло бы описывать эволюционную историю, обычно эту возможность игнорируют.

Вопросы для самопроверки:

– Каково было бы эволюционное значение вершины в дереве, где встречаются четыре ребра (то есть, где маршрут из одного ребра расходится на три направления)? Можете ли представить себе правдоподобные обстоятельства, при которых несколько видов могут расходиться таким образом?

Хотя в идеале каждое филогенетическое дерево должно иметь корень, показывающий общего предка таксонов, иногда приходится обходиться без него. Некоторые методы филогенетического построения деревьев дают некорневые деревья. Например, на рисунке 5.2 показано некорневое дерево и несколько корневых деревьев, которые с ним согласуются. Два дерева справа могли быть согнуты и растянуты, чтобы выглядеть как дерево слева; их отличает только расположение корня.

Рисунок 5.2. Некорневое дерево (слева) и две его корневые версии (в центра и справа).

Посмотрим на деревья с топологической точки зрения. Дерево, относящееся к ряду таксонов, может фактически указывать несколько различных типов информации об их отношениях. Во-первых, если не указываем длины ребер, а значит, смотрим только на ветвящуюся структуру, то рассматриваем только топологию дерева. Считается, что два дерева топологически одинаковы, если можно согнуть и растянуть ребра одного из них, чтобы получить второе дерево. Однако нельзя отрезать ребро и снова прикреплять его в другом месте; это может дать дерево, которое топологически отличается от исходного.

На рисунке 5.3 деревья , и топологически совпадают с некорневыми деревьями, потому что, если бы какая-либо из этих фигур была сделана из резины, ее можно было бы деформировать в другие, не разрезая и не склеивая куски вместе. Дерево , напротив, топологически отличается от , и .

Для корневых деревьев используем аналогичную концепцию. Два корневых дерева топологически эквивалентны, если одно можно преобразовать в другое, не перемещая корень. Можно изменить длину ребер, но не структуру ветвления.

Рисунок 5.3. Четыре топологических дерева; как некорневые деревья, все, кроме правого нижнего, они идентичны.

Вопросы для самопроверки:

– Как на рисунке 5.3 расположить корень дерева , чтобы полученное дерево не было топологически эквивалентным корневому дереву ? А чтобы получилось топологически то же самое, что и корневое дерево ?

Топологическое дерево, даже некорневое, довольно многое говорит об эволюционной истории таксонов, к которым оно относится. Например, все деревья на рисунке 5.2 показывают, что таксоны и связаны одним разделением линии, точно так же как и . Тем не менее, несколько раздвоений линии произошли между и , эволюционировавших от общего предка, поскольку в процессе возникли два других таксона.

Знание местоположения корня передает больше информации и может дать лучшее представление о порядке событий во времени. Например, изображенное справа на рисунке 5.2 дерево однозначно задаёт следующий порядок бифуркаций: общий предок дал начало двум таксонам, один из которых, возможно, эволюционировал дальше, чтобы стать ; другой впоследствии породил и третий таксон; этот третий таксон затем породил и .

Дерево в центре рисунка 5.2 можно интерпретировать аналогичным образом. Общий предок дал начало двум таксонам, один из которых дал начало как , так и , в то время как другой дал начало и . Обратите внимание, однако, что только с топологическим деревом не можем сказать, какое из этих двух последних бифуркации произошло первым: существовал ли самый последний общий предок и более поздний, чем и ? Нет возможности определить это по дереву.

Количество различных топологических деревьев, которые могут соотносить несколько терминальных таксонов, быстро растёт с увеличением числа таксонов. Например, существует только 1 некорневое топологическое дерево, относящееся к 3 таксонам, но есть 3 некорневых топологически различных дерева, относящиеся к 4 таксонам.

Вопросы для самопроверки:

– Нарисуйте одно некорневое топологическое дерево, которое может относиться к терминальным таксонам , и . Нарисуйте три некорневых топологических дерева, которые могут относиться к терминальным таксонам , , и .

На 5 терминальных таксонов приходится 15 таких деревьев. Таким образом, если не принимать во внимание местонахождение корня, существует на 13 деревьев, которые могут связать 5 гоминоидов, а больше, чем было представлено во введении к главе. Для 6 терминальных таксонов насчитывается более 100 возможных некорневых деревьев. По мере увеличения числа таксонов количество деревьев быстро вырастает до астрономических размеров. В упражнениях найдете точные формулы, определяющие количество некорневых и корневых деревьев, относящихся к таксонам. Также увидите, насколько велики эти числа, даже для относительно небольшого числа таксонов. Большое количество деревьев вызывает дискомфорт, потому что это означает, что некоторые подходы к поиску хорошего дерева для соотнесения таксонов будут медленными. Если метод находит «лучшее» дерево, рассматривая каждое возможное дерево по отдельности, то его использование будет чрезвычайно трудоемким, когда задействовано много таксонов.

На помощь в решении обозначенной проблемы поиска лучшей классификации приходят метрические деревья. В дополнение к топологической структуре дерево может иметь метрическую структуру; каждому ребру может быть присвоена определенная длина. Эта метрическая структура может быть задана путем записи чисел для обозначения длин рядом с ребрами (см. Рисунок 5.4 (слева)), или ребро может быть наглядно представлено путем рисования дерева с ребрами соответствующей длины, но без их явной нумерации. Таким образом, топологическое дерево и немаркированное метрическое дерево неотличимы друг от друга. Для ясности, будем маркировать ребра их длиной, когда нужно задать метрическое дерево.

Как правило, длины ребер в филогенетическом дереве, построенном из данных последовательности ДНК, каким-то образом представляют собой количество мутаций, которые произошли между расщеплениями линии. Чем длиннее ребро, тем больше последовательность ДНК мутировала в ходе эволюции, которую представляет это ребро.

Если, например, модель Джукса-Кантора замещения оснований адекватно описала эволюцию нескольких таксонов, то длина ребра в дереве, относящемся к ним, может быть расстоянием Джукса-Кантора между последовательностями на двух концах. Как видели в главе 4, это расстояние представляет собой среднее число замен оснований на сайт, произошедших при происхождении новой последовательности. Сюда включены мутации, скрытые другими мутациями, для оценки которых была разработана формула расстояния. Поскольку расстояние Джукса-Кантора является аддитивным и симметричным, общее расстояние между двумя таксонами вдоль дерева должно быть расстоянием Джукса-Кантора между ними.

Если предположение о молекулярных часах справедливо для эволюции связанных последовательностей, то расстояния в дереве имеют постоянное значение. Напомним, что молекулярные часы просто означают, что скорость мутаций постоянна для всех рассматриваемых линий. Если обозначает скорость мутации, измеряемую, например, в количестве произошедших за год замен оснований на сайт, а обозначает время в годах, то количество мутаций, которое произойдет в течение этого времени, составляет базовых замен на сайт.

Таким образом, молекулярные часы означают, что количество мутаций на любом ребре пропорционально прошедшему времени, при этом константа пропорциональности представляет собой постоянную скорость мутации. Если предположить, что существуют молекулярные часы, то независимо от того, рисуем ли длины ребер, представляющие количество мутаций или только прошедшее время, то нарисуем одну и ту же фигуру с точностью до масштаба этой константы.

Если гипотеза молекулярных часов справедлива для корневого метрического дерева, то каждый лист будет расположен на одинаковом общем расстоянии от корня дерева. Это связано с тем, что расстояния от корня пропорциональны времени, прошедшему с тех пор, как таксоны начали расходиться с общим предком. У каждого таксона было одинаковое количество времени, чтобы эволюционировать от корневого предка, поэтому каждый таксон накопит одинаковое количество мутаций.

Без молекулярных часов связь между количеством мутаций вдоль ребра и количеством времени может быть сложной для моделирования. Предположим, что вдоль одного ребра филогенетического дерева частота мутаций была довольно мала, а вдоль другого – частота мутаций была большой. Затем несмотря на то, что оба края могут соответствовать одинаковому количеству времени, вдоль одного из них произойдет значительно больше мутаций. Без получения какой-либо дополнительной информации о скорости мутации – возможно, путем сравнения с летописью окаменелостей – обычно нет способов определения прошедшего времени, связанного с ребрами деревьев.

Метрические деревья иногда рисуются в «квадратном» стиле, чтобы было легче сравнивать расстояния по различным эволюционным путям. Например, два дерева на рисунке 5.4 представляют одну и ту же информацию. В дереве слева ребра имеют указанную длину, а в дереве справа горизонтальные ребра имеют те же длины. Таким образом, вертикальные ребра на правом дереве считываются как не вносящие никакого вклада в количество мутаций; они служат исключительно для разделения различных линий для повышения читабельности.

Рисунок 5.4. Разные изображения одного и того же метрического дерева.

Задачи для самостоятельного решения:

5.1.1. Рассмотрим деревья на рисунке 5.5.

Рисунок 5.5. Деревья для задачи 5.1.1.

а. Какие из них совпадают с корневыми метрическими деревьями?

б. Какие из них совпадают с некорневыми метрическими деревьями?

в. Какие из них такие же, как корневые топологические деревья?

г. Какие из них такие же, как некорневые топологические деревья?

д. Для каких деревьев работают молекулярные часы?

5.1.2. а. Нарисуйте единственное топологически уникальное некорневое раздвоенное дерево, которое могло бы описать связь между 3 таксонами.

б. Нарисуйте три топологически различных корневых раздвоенных дерева, которые могли бы описать связь между 3 таксонами.

5.1.3. а. Нарисуйте все 3 топологически различных некорневых раздвоенных деревьев, которые могли бы описать связь между 4 таксонами.

б. Нарисуйте все 15 топологически различных корневых раздвоенных деревьев, которые могли бы описать связь между 4 таксонами.

5.1.4. Для терминальных таксонов количество некорневых раздвоенных деревьев можно найти как . Составьте таблицу значений и отобразите эту функцию для .

5.1.5. Для терминальных таксонов количество корневых раздвоенных деревьев равно значению . Составьте таблицу значений и отобразите эту функцию для .

5.1.6. В этой задаче рассмотрим рассуждения, лежащие в основе формул для числа топологически различных деревьев, корневых и некорневых.

а. Предположим известно, что некорневое дерево с концевыми вершинами состоит из ребер. Объясните, почему некорневое дерево с концевыми вершинами будет иметь ребра. Подсказка: подумайте о том, как добавление еще одной конечной вершины в существующее дерево влияет на количество ребер.

б. Поскольку некорневое дерево с 2 концевыми вершинами имеет 1 ребро, объясните из пункта (а), почему некорневое дерево с концевыми вершинами будет иметь ребра.

в. Предположим известно, что существует некорневых деревьев с концевыми вершинами. Объясните, почему существует некорневых деревьев с концевой вершиной. Подсказка: подумайте, сколькими различными способами можно добавить еще одну конечную вершину к существующему дереву.

г. Поскольку существует только 1 некорневое дерево с 2 концевыми вершинами, объясните используя пункт (c), почему существует некорневых деревьев с концевыми вершинами при .

д. Объясните, почему .

е. Почему число корневых деревьев с концевыми вершинами такое же, как число некорневых деревьев с концевыми вершинами?

ж. Сделайте вывод о правильности формул в задачах 5.1.4 и 5.1.5.

5.1.7. Поскольку митохондриальная ДНК у человека наследуется исключительно от матери, она может быть использована для структуры, относящейся к любому количеству людей из разных этнических групп, предполагая, что все люди произошли от одной первой человеческой самки. В зависимости от модели кластеризации этнических групп, это может дать представление о физическом местоположении той женщины, которую иногда называют митохондриальной Евой.

В работе Канна 1987 года была впервые предпринята попытка определить местонахождение митохондриальной Евы в Африке. Поддерживая теорию происхождения человека «из Африки», было построено дерево с корнями, которое, как утверждается, показывает отношения между 147 людьми. Сколько топологически различных деревьев нужно было бы рассмотреть, если бы действительно рассматривалась каждая возможность? Возможно, для ответа на этот вопрос придется использовать формулу Стирлинга: . Здесь символ «∼» можно интерпретировать как «приблизительно». Изучению последствий трудности рассмотрения стольких деревьев посвятил свою работу Гиббонс в 1992 году.

5.1.8. Филогенез четырех терминальных таксонов A, B, C и D связан по определенному метрическому дереву. Суммарные расстояния между таксонами вдоль дерева оказались такими же, как в таблице 5.1.

Таблица 5.1. Расстояния между таксонами для задачи 5.1.8

A B C D

A .6 .6 .2

B .4 .6

C .6

а. Используя любой подход, который пожелаете, определите правильное некорневое дерево, относящееся к этим таксонам, а также все длины его ребер. Объясните, как исключили другие топологические деревья.

б. Можете ли определить корень дерева по этим данным? Объясните, почему да или почему нет.

Примечание: Методы решения такого рода проблем являются предметом следующих разделов.

5.2. Построение дерева дистанционными методами UPGMA и FM

При построении филогенетического дерева таксоны, которые хотим связать, обычно являются теми, которые живут в настоящее время. Есть информация, такая как последовательности ДНК, от терминальных таксонов и нет информации от тех, которые представлены внутренними вершинами. В действительности, даже не знаем, какие внутренние вершины должны существовать, потому что не знаем даже топологию дерева.

Первым классом методов построения филогенетических деревьев, которые обсудим, являются дистанционные методы. Они пытаются построить дерево, используя информацию, которая предположительно описывает общие расстояния между терминальными таксонами вдоль дерева.

Чтобы понять, как получить эти расстояния, представьте, что пытаемся найти эволюционные отношения четырех видов: , , и . Выбирая тот или иной ортологичный участок ДНК из их геномов, получаем и выравниваем последовательности из каждого. Если модель замены оснований Джукса-Кантора, рассмотренная в главе 4, кажется подходящей для имеющихся данных, то вычисляем расстояния Джукса-Кантора между каждой парой последовательностей. Получатся оценки расстояний по дереву, которые сводим в Таблицу 5.2.

В зависимости от данных последовательности могли бы вместо этого принять другую модель подстановки оснований, что привело бы к использованию другой формулы расстояния, такой как в 2-параметрической модели Кимуры или логарифмическое расстояние. Несмотря на это, расстояние, которое вычисляем между последовательностями, считается мерой количества произошедших мутаций. Если бы эти расстояния были точной мерой количества произведенных мутаций, они бы соответствовали между конечными таксонами в найденном метрическом дереве.

Таблица 5.2. Расстояния между таксонами

.45 .27 .53

.40 .50

.62

На самом деле даже не ожидаем найти дерево, которое точно соответствует имеющимся данным; в конце концов, расстояния выводятся из данных последовательности и не должны быть точно правильными. Более того, метод вывода расстояний зависел от модели, которая включала дополнительные предположения, которые, безусловно, не встречаются в реальных организмах. Надеемся, однако, что построенное дерево не будет слишком чувствительно к такого рода ошибкам на больших расстояниях.

Первый метод, который рассматриваем, называется методом среднего расстояния или, более формально, невзвешенным парно-групповым методом с арифметическими средними (UPGMA). Этот метод создает корневое дерево и предполагает наличие молекулярных часов. Самый простой способ понять алгоритм – это ознакомиться с примером его использования.

По приведенной выше таблицы данных выберем два ближайших таксона, и . Поскольку они находятся на расстоянии 0,27 друг от друга, изобразим на рисунке 5.6 каждое ребро с длиной .

Рисунок 5.6. UPGMA; шаг 1.

Затем объединяем и в группу и усредняем расстояния и до каждого отдельного таксона, чтобы получить расстояние от группы до этого таксона. Например, расстояние между группой и равно , а расстояние между и равно . Таким образом, исходная таблица сводится к таблице 5.3.

Таблица 5.3. Расстояния между групп; UPGMA, Шаг 1

.425 .575

.50

Теперь просто повторяем процесс, используя расстояния в таблице 5.3. Поскольку ближайшими таксонами и/или группами в новой таблице являются и , которые находятся на расстоянии 0,425 друг от друга, то получаем рисунок 5.7.

Рисунок 5.7. UPGMA; шаг 2.

Ребро должно иметь длину , в то время как другое новое ребро должно иметь длину , потому что уже есть ребро длины для учета некоторого расстояния между и другими таксонами.

Снова объединив таксоны, формируем группу и вычисляем расстояние от неё до путем усреднения исходных расстояний от до каждого из , и . Это приводит к значению . Обратите внимание, что это не то же самое, что усреднение расстояния от до и до . Поскольку новая таблица расстояний будет иметь это значение в качестве единственной записи, нет необходимости приводить ее. Изобразим рисунок 5.8, считая, что расстояние от корня до равно . Конечное ребро имеет длину. 0625, таким образом, помещаем оставшийся таксон на расстоянии от корня.

Рисунок 5.8. UPGMA; шаг 3.

Как и подозревали, дерево, которое построили для имеющихся данных, не совсем соответствует этим данным. Расстояние на дереве от до , например, равно , хотя по исходным данным должно быть . Тем не менее, расстояния между вершинами построенного дерева, по крайней мере, достаточно близки к расстояниям, указанным в исходных табличных данных.

Если бы было больше таксонов, то пришлось бы сделать больше шагов для завершения процесса UPGMA, но не было бы никаких принципиально новых действий. На каждом шаге объединяем два ближайших таксона или группы вместе, всегда размещая их на равных расстояниях от общего предка. Затем сворачиваем объединенные таксоны в группу, используя усреднение для вычисления расстояния от этой группы до таксонов и групп, которые еще предстоит объединить. Один момент, с которым следует быть особенно осторожным, заключается в том, что при вычислении расстояний между двумя группами нужно усреднить все расстояния от членов одной группы до членов другой – если одна группа имеет членов, а другая имеет членов, придется усреднить расстояний. Каждый шаг алгоритма уменьшает размер таблицы расстояний на единицу, так что после достаточного количества шагов все таксоны объединяются в единое дерево.

Обратите внимание, что предположение о молекулярных часах неявно присутствовала в UPGMA. В примере, когда поместили и на концы ветвей одинаковой длины, предположили, что количество мутаций, которые каждый из них претерпел от своего общего предка, было одинаковым. Метод UPGMA всегда размещает все таксоны на одинаковом расстоянии от корня, так что количество мутаций от корня до любого таксона одинаково.

Вторым рассмотрим алгоритм Фитча-Марголиаша. Этот метод немного сложнее, чем UPGMA, но основан на том же подходе. Тем не менее, попытаемся отказаться от предположения UPGMA о молекулярных часах.

Прежде чем изложить алгоритм, сделаем несколько математических наблюдений. Во-первых, если попытаемся поместить 3 таксона на некорневое дерево, то будет только одна топология, которую необходимо учитывать. Кроме того, для 3 таксонов можем назначить желаемые длины ребер, чтобы точно соответствовать данным. Чтобы убедиться в этом, рассмотрим дерево на рисунке 5.9. Если есть некоторые данные о расстоянии , и , то можно составить систему уравнений , , .

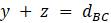Эти уравнения могут быть решены либо путем записи системы в виде матричного уравнения и нахождения обратной матрицы, либо путем подстановки формулы для одной переменной, полученной из одного уравнения, в другие. Любой способ гарантированно приведёт к следующему решению , , .

Рисунок 5.9. Некорневое 3-таксонное дерево.

Будем называть эти формулы 3-точечными формулами для подгонки таксонов к дереву. К сожалению, с более чем 3 таксонами точная подгонка данных к дереву обычно невозможна. Однако алгоритм Фитча-Марголиаша (кратко называемый в таблицах как FM) использует случай 3 таксонов для обработки большего количества таксонов. Теперь объясним работу алгоритма на примере. Будем использовать данные о расстоянии, приведенные в таблице 5.4.

Таблица 5.4. Расстояния между таксонами

.31 1.01 .75 1.03

1.00 .69 .90

.61 .42

.37

Начинаем с выбора ближайшей пары таксонов для присоединения, как это делали в UPGMA. Глядя на таблицу расстояний, и являются первой парой, которая соединится. Чтобы соединить их, не помещая их на равное расстояние от общего предка, временно сводим задачу к случаю 3-таксонов, объединяя все остальные таксоны в группу. Таким образом, для имеющихся данных вводим группу . Находим расстояние от каждого из и до группы, усредняя их расстояния до каждого члена группы. Таким образом, расстояние от до равно , в то время как от до оно равно . Это дает таблицу 5.5.

Таблица 5.5. Расстояния между группами; FM-алгоритм, шаг 1a

.31 .93

.863

Имея только три таксона в этой таблице, можем точно подогнать данные к дереву, используя 3-точечные формулы, чтобы получить рисунок 5.10. Ключевым моментом здесь является то, что 3-точечные формулы, в отличие от UPGMA, могут давать неравные расстояния таксонов от общего предка.

Рисунок 5.10. FM-алгоритм; шаг 1.

Теперь оставляем только ребра, заканчивающиеся в и на рисунке 5.10, и возвращаемся к исходным данным. Помните, что группа была нужна только временно, чтобы могли использовать 3-точечные формулы; пока не собирались объединять эти таксоны. Однако, поскольку объединили и , объединяем их в группу для остальной части алгоритма, как сделали бы с UPGMA. Это формирует таблицу 5.6.

Таблица 5.6. Расстояния между группами; FM-алгоритм, шаг 1b

1.005 .72 .965

.61 .42

.37

Снова ищем ближайшую пару (теперь это и ) и соединяем их аналогичным образом. Объединяем все, кроме и , в одну временную группу и вычисляем расстояния и . Полученными значениями заполняем таблицу 5.7. Применение трехточечной формулы к таблице 5.7 дает рисунок 5.11.

Таблица 5.7. Расстояния между группами; FM-алгоритм, шаг 2a

.683 .783

.37

Рисунок 5.11. FM-алгоритм; шаг 2.

Оставляем ребра инцидентные с и на рисунке 5.11, отбрасывая ребро, ведущие к временной группе . Таким образом, теперь есть две объединенные группы, и . Чтобы вычислить новую таблицу, содержащую эти две найденные группы, усредняем расстояния и . Выше уже вычислили , поэтому получаем таблицу 5.8.

Таблица 5.8. Расстояния между группами; FM-алгоритм, шаг 2b

1.005 .8425

.515

На этом этапе можем получить итоговое дерево по таблице путем окончательного применения 3-точечных формул, что дает рисунок 5.12.

Рисунок 5.12. FM-алгоритм; шаг 3.

Теперь заменяем группы на этой последней диаграмме шаблонами ветвления, которые уже нашли ранее. Это дает рисунок 5.13.

Последним шагом является заполнение оставшихся длин и , используя длины, показанные на рисунке 5.12. Так как и в среднем дают расстояние от соединяющей их вершины, а и находятся в среднем на от соединяющей их вершины, то и получаем для присвоения длин оставшимся ребрам.

Рисунок 5.13. FM-алгоритм; завершение.

Обратите внимание, что одно ребро оказалось отрицательной длины. Поскольку этого не может быть, многие на практике предпочли бы просто переопределить длину в 0. Однако, если это произойдет, то должны будем по крайней мере проверить, что отрицательная длина была близка к 0, иначе придётся беспокоиться о качестве используемых данных.